Your McMullen carpet

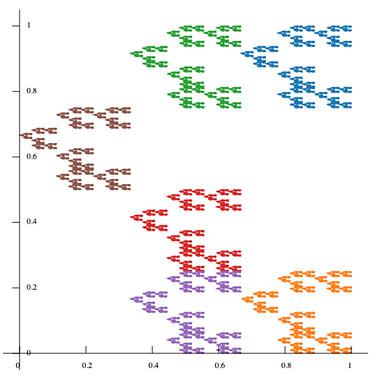
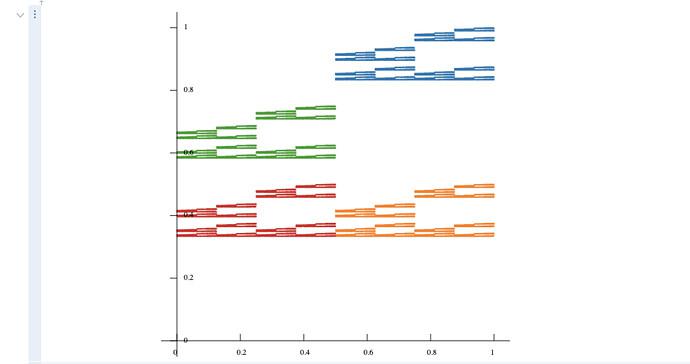
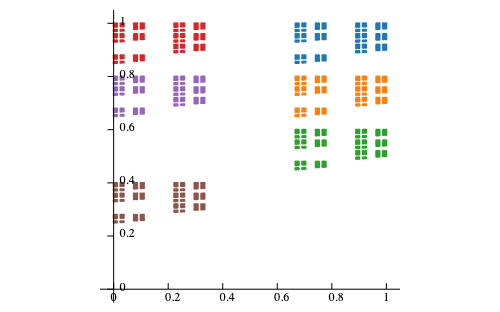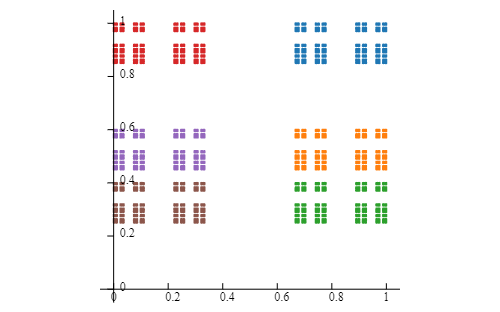(10 pts)

In this problem, you’re going to generate and analyze your own McMullen Carpet. Specifically, given a skelatal description of a McMullen Carpet, you will

1. Generate a detailed image of the carpet using this Observable notebook and
2. Compute the box-counting dimension of the carpet using McMullen’s formula.

To view the skeleton of your McMullen Carpet, choose your name from the list below:

1. Here is the generated image of my carpet:

2. My box-counting dimension using McMullen’s formula ended up as:
   \dim(C) = \frac{\log(2)}{\log(3)} + \frac{\log(\frac{6}{2})}{\log(5)}=\frac{\log(2)}{\log(3)} + \frac{\log(3)}{\log(5)}\approx 1.3135

I was able to generate this picture

And computed my dimension using:

My McMullen Carpet’s image is:

The box counting dimension using parameters M=3, N=6, m=3, n=5 is \dim(C) = \frac{\log(3)}{\log(3)} + \frac{\log(6/3)}{\log(5)} \approx 1.43.

The generated image of my carpet:

My box-counting dimension using McMullen’s formula:

My Mcmullen Carpet:

Screen Shot 2021-11-15 at 11.18.13 AM1133×1130 141 KB

Using the box counting method to calculate the dimension gave me:
dim(C) = \frac{log(3)}{log(3)}+\frac{log(\frac{6}{3})}{log(4)}=1+.5=1.5

1. Here is the generated image of my carpet:
   
   

   Screen Shot 2021-11-15 at 12.20.39 PM2176×1150 113 KB
2. My box-counting using McMullen’s formula ended up as:
   dim(C)= \frac{log(2)}{log(2)} + \frac{log(\frac{4}{2})}{log(4)} = 1.5