(10 pts)
In this problem, you’re going to find the super-attracting parameters for the periodic orbits of period five for your own personal family of quadratics. To get the precise statement of your problem, choose your name from the list below.
For the function f_c(x)=2c+\frac{x^2}{2} I found the super-attracting parameters of period 5 to be
[(-1.98542425305421, 1),
(-1.86078252220485, 1),
(-1.62541372512330, 1),
(0.000000000000000, 1)]
The critical point of f_c, used as x_0 while graphing the cobweb plot, was 0.
When using the parameter value c= -1.86078252220485, the cobweb plot demonstrated an attractrive periodic orbit of 5.
Sage code :Sage Cell Server
Using the code above, I found the super-attracting parameters for period 5 for my family of functions:
f_c(x)=2c + \frac{x^2}{2} -3x + \frac{15}{2}
The critical point for my family f_c is x_0=3
Using the smallest absolute value parameter for c that is non-zero, where c=-1.62541372512330 the cobweb plot showing a periodic orbit of 5 is as follows:
For the function f_c(x)=c+x^2-6x+12 I found the super-attractive parameters of period 5 to be: c = -1.86078252220485 and c = -1.62541372512330
The critical point of f_c is x_0=3
When using the parameter c=-1.86078252220485, the cobweb plot appears as follows:
For f_c(x)=2c+\frac{x^2}{2}-x+\frac{3}{2}, using this Sage Code, with x_0=1, I determined the super-attracting parameters of period 5 to be
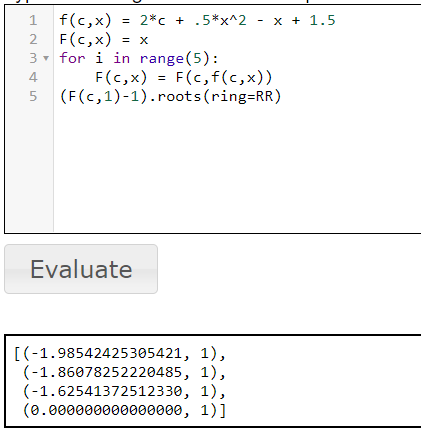
I then selected c=-1.62541372512330 as the parameter with the smallest absolute value and generated the following cobweb plot, which shows a periodic orbit of period 5:
Take a look at the discussion here. Also I need a link to your Sage code - not mine. You can get that from the “Share” button on the right of the screen.
Given the function f_c(x)=x^2-8x+20+c, with x_0=4, I found my super-attracting parameter for period 5 to be c=
[(-1.98542425305421, 1),
(-1.86078252220485, 1),
(-1.62541372512330, 1),
(0.000000000000000, 1)],
using this Sage Cell Server .
Using the smallest absolute value of c that is non-zero, where c = -1.62541372512330, the cobweb plot clearly shows an attractive orbit of period 5.
