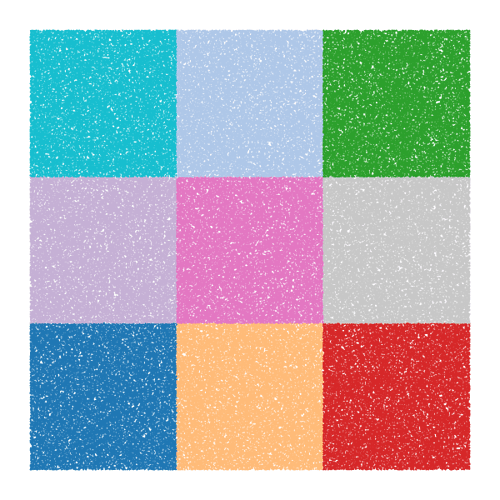(5 pts)
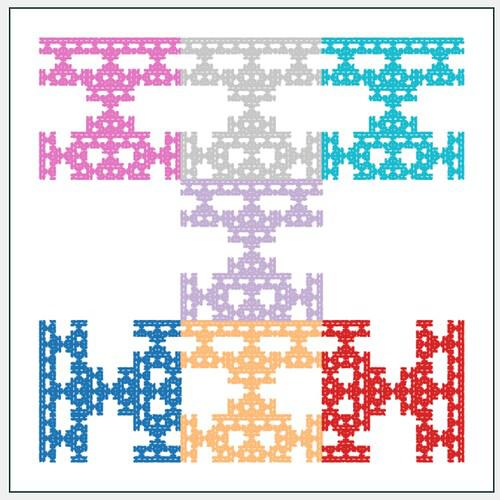
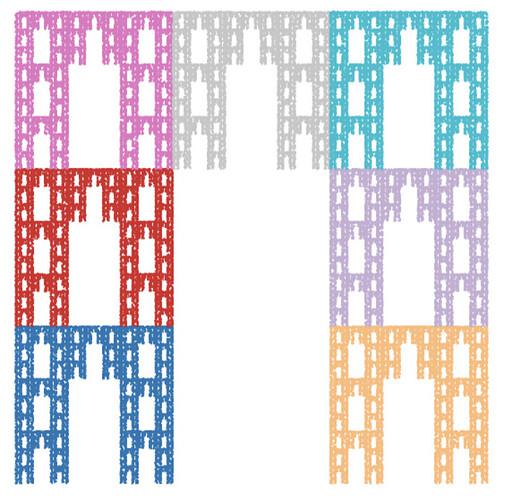
In this problem, your mission is to generate the image of a self-similar set obtained by modifying a nine function IFS for the square. Consider, for example, the three images below.
The first is clearly a square expressed as a self-similar set consisting of nine parts. The second is the Sierpinski carpet obtained by removing the central square from the original large square. The last is a bit groovier looking and is obtained by removing the four North, East, South, and West squares from the original and rotating the central square through the angle 45^{\circ}.
A simple way to write down the IFS for the square (if you want to be able to easily incorporate rotation into the individual pieces) is as:
[
shift([-1, -1]).compose(scale(1 / 3)),
shift([0, -1]).compose(scale(1 / 3)),
shift([1, -1]).compose(scale(1 / 3)),
shift([-1, 0]).compose(scale(1 / 3)),
shift([0, 0]).compose(scale(1 / 3)),
shift([1, 0]).compose(scale(1 / 3)),
shift([-1, 1]).compose(scale(1 / 3)),
shift([0, 1]).compose(scale(1 / 3)),
shift([1, 1]).compose(scale(1 / 3))
]
If you paste that into the IFS Visualizer, crank up the number of points to 250000, check the color box, and leave the algorithm set to Random, you should get an image like the following:
If we’d like to generate the Sierpinski carpet, we could simply remove the function that shifts by [0,0]. To generate the third image, we would need to remove four of the functions from the square IFS and slap a .compose(rotate(45*degree)) onto the central function.
Again, your mission is to find an IFS to generate a picture that’s something like one of these. To view your target image, select your name from the list below: