mark
(10 pts)
In this assignment, you’ll find a function \varphi that conjugates a given function g to another function f. Choose your name from the drop down menu below for the specifics:
An archived instance of a Chaos and Fractals forum
Find a conjugation
lee7
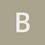
A.
For the functions f(x)=3x-3x^2 and g(x)=x^2+13x+35 , I found a conjugacy \varphi(x) =- \frac{1}{3}x - \frac{5}{3}
Directly evaluating:
f \circ \varphi = 3( - \frac{1}{3}x - \frac{5}{3})-3(- \frac{1}{3}x - \frac{5}{3})^2
f \circ \varphi = - \frac{x^2}{3}- \frac{13}{3}x-\frac{40}{3}
and
\varphi \circ g = -\frac{x^2}{3}+13 (\frac{-x}{3})+35(\frac{-1}{3})-\frac{40}{3}
\varphi \circ g = - \frac{x^2}{3}- \frac{13}{3}x-\frac{40}{3}
Thus, f \circ \varphi = \varphi \circ g.
B.
The function’s cobweb plots behave similarly when beginning from their respective critical points, indicating the functions may be related to one another through a conjugation function.
Note that the functions are inverted and scaled differently.
ofeldman
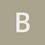
For the functions f(x)=4x-4x^2 and g(x)=x^2+8x+10, I found a conjugacy \varphi(x)=-\frac{1}{4}x-\frac{1}{2}.
Directly evaluating:
f\circ\varphi=4(-\frac{1}{4}-\frac{1}{2})-4(-\frac{1}{4}x-\frac{1}{2})^2
f\circ\varphi=-\frac{1}{4}x^2-2x-3
and
\varphi\circ g=-\frac{1}{4}(x^2+8x+10)-\frac{1}{2}
\varphi\circ g=-\frac{1}{4}x^2-2x-3
Thus f\circ\varphi=\varphi\circ g.
The cobweb plots of the two functions behave similarly when they start orbiting from their critical points. The two function’s are inverted, scaled, and translated.
scowart
a. Let
f(x)=4x-4x^2 \space\text{and}\space g(x)=-\frac{4}{3}x^2-\frac{20}{3}x-\frac{28}{3}.
Consider the conjugacy \varphi(x)=3x-4. Evaluating \varphi\space\circ\space f we see,
\varphi\space\circ\space f=\varphi(f(x))\\
=3(4x-4x^2)-4\\
=-12x^2+12x-4.
Now we check g\space\circ\space\varphi,
g\space\circ\space\varphi=g(\varphi(x))\\
=-\frac{4}{3}(3x-4)^2-\frac{20}{3}(3x-4)-\frac{28}{3}\\
=-\frac{4}{3}(9x^2-24x+16)-\frac{20}{3}(3x-4)-\frac{28}{3}\\
=-12x^2+32x-\frac{64}{3}-20x+\frac{80}{3}-\frac{28}{3}\\
=-12x^2+12x-4.
Thus, since g\space\circ\space\varphi =\varphi\space\circ\space f, \varphi is a conjugacy from g to f.
b.
badler
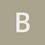
My functions: f(x)=3x-3x^2 and g(x)=\frac{3x^2}{4} +\frac{21x}{2} +\frac{115}{4}
I found a conjugacy \varphi(x)=-\frac{1}{4}x -\frac{5}{4}.
I decided to directly evaluate f \circ \varphi and \varphi \circ g instead of g \circ \varphi and \varphi \circ f because it made my computations a little easier and it still worked since I kept my order consistent.
Directly evaluating:
f \circ \varphi=3(-\frac{1}{4}x - \frac{5}{4}) -3(-\frac{1}{4}x - \frac{5}{4})^2
f \circ \varphi=-\frac{3}{16}x^2 -\frac{21}{8}x -\frac{135}{16}
and
\varphi \circ g=-\frac{1}{4}(\frac{3x^2}{4} +\frac{21x}{2} +\frac{115}{4})-\frac{5}{4}
\varphi \circ g-\frac{3}{16}x^2 -\frac{21}{8}x -\frac{135}{16}
Thus, f \circ \varphi=\varphi \circ g.
Using 2 side by side cobweb plots it is easy to see the geometric similarity of the critical orbits of f and g.
type or paste code here
pikenber
a. Given f(x) = x^2 - 1 and g(x) = \frac {x^2}{4}+\frac{5x}{2}-\frac{11}{4}, consider the conjugate function \varphi(x)=4x-5.
Directly evaluating \varphi \circ f, we see:
\varphi \circ f =4(x^2-1)-5=4x^2-4-5=4x^2-9.
Evaluating g\circ\varphi = \frac {(4x-5)^2}{4}+\frac{5(4x-5)}{2}-\frac{11}{4} =4x^2-10x+\frac{25}{4}+10x-\frac{25}{2}-\frac{11}{4}
=4x^2-9, which shows \varphi\circ f=g\circ\varphi.
b. Beginning at their critical points, the cobweb plots for these functions both show the same activity, which in this case is a period 2 orbit.
mark