Exploring a personally chosen tile

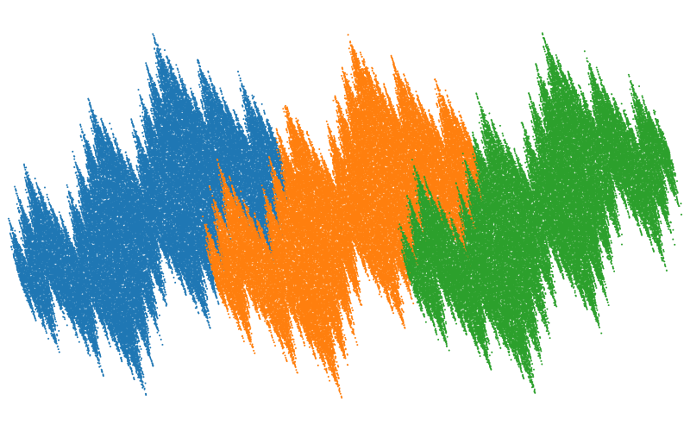
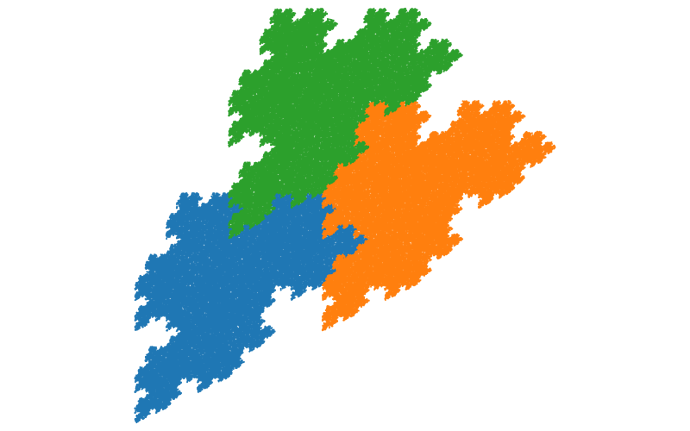
(15 pts)

In this final forum assignment, you’re going to explore a fractal tiling problem that I’ve generated personally for you. In all cases you should

• Make it clear what was asked of you
• Include any matrix and digit set that you used (as computer code is sufficient)
• Include any images that you were asked to generate.

All of you will use this tutorial on generating self-affine tiles:

To get your problem, choose your name from the list below:

1. Generate rotationally symmetric Gospoer flake:
   \begin{pmatrix} 1 & -2 \\ 2 & 3 \end{pmatrix}

Screen Shot 2021-12-06 at 12.07.16 PM1520×1035 81 KB

2. Modify the digit set so that the middle piece is missing:
   I took out the vector: [0,0] from the digit set because it corresponded to the middle piece.
   
   

   Screen Shot 2021-12-06 at 12.08.14 PM1206×1049 110 KB

I was asked to generate a fractal tile consisting of three copies of itself all lined us in a row given a picture of the digit base set in the plane. Based on that digit set, my matrix is \begin{pmatrix} 2 & 1 \\ 1 & -1 \end{pmatrix}. The corresponding tile generated looks like this:

basic_picture (1)800×500 91 KB

which is in fact three copies of itself lined up in a row.

For the matrix:
A= \begin{pmatrix} -1 & 2\\ 1 & 1 \end{pmatrix}

1. Generate the basic time with three parts
   

   

   basic_picture (1)800×500 29.4 KB

2. Generate an image of the rotationally symmetric version using a change of basis matrix.
   

   

   different_basis (1)800×500 25.4 KB

*updated picture

Using the matrix
A= \begin{pmatrix} 3 & 0 \\ 0 & 2\end{pmatrix}
and the digit set
\begin{pmatrix} 0 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \begin{pmatrix} 1 \\ 2 \end{pmatrix}, \begin{pmatrix} 1 \\ -1 \end{pmatrix}, \begin{pmatrix} 2 \\ 0 \end{pmatrix}, \begin{pmatrix} 2 \\ 1 \end{pmatrix}.

I was able to produce this image

differentD800×500 35.8 KB

1. The basic tile with five parts generated from the matrix \begin{pmatrix} 2 & -1 \\ 1 & 2 \end{pmatrix} was
   

   basic_picture (2)800×500 82.5 KB
   
   with the digit set
   D = [[0,0], [1,0], [1,1], [2,0],[2,1]]
2. Next, I modified the digit set so that the resulting tile has four fold rotational symmetry
   D by removing the [0,0]
   D = [ [1,0], [1,1], [2,0], [2,1]]
   This gave me the tile
   
   

   differentD800×500 42.2 KB

My question asked that I generate my tile using the matrix \begin{pmatrix} 3 & 0 \\ 0 & 2 \end{pmatrix}.

Using the digit set: D = [[0, 0], [0, 1], [1, 0], [1, 1], [2,0], [2,1]], I generated the following image:

basic_picture800×500 261 KB

After modifying my digit set to: D = [[0,0], [0,1], [1,2], [1,1], [2,0], [2,1]], I attained:

differentD (1)800×500 35.3 KB

Generate a Tame Twindragon using A = \begin{pmatrix} 1 & 2 \\ -1 & 0 \end{pmatrix}.

1. The first iterate does not render because it is non-contractive.
2. This can be circumvented by rendering a higher iterate, which is contractive.

The second iterate is:

image800×500 121 KB