Sketch solutions of an autonomous equation
(10 points)
For this problem, you're going to sketch some solutions for a first order, autonomous equation together with several solutions between the equilibria. To obtain your personal function, go to the homework on "First order ODEs" listed on our class webpage. You should see a box to type in your forum username to get the right hand side of your very own autonomous equation. From there you should type a response to this post that
- Identifies the equilibrium solutions (with LaTeX in your post)
- Draw the equilibrium solutions with pencil and paper, and
- Draw on that same paper a solution between each pair of equilibria, as well as two unbounded solutions, and
- Scan or take a picture of your drawing to upload as part of your answer.
Comments
The autonomous equation I received was: $$f(y)=-(y-2)(y+2)(y+3)^2$$
The equilibrium solutions of this equation include $y=-3,-2,2$ with multiplicity 2 at $y=-3.$
The equation I received was:
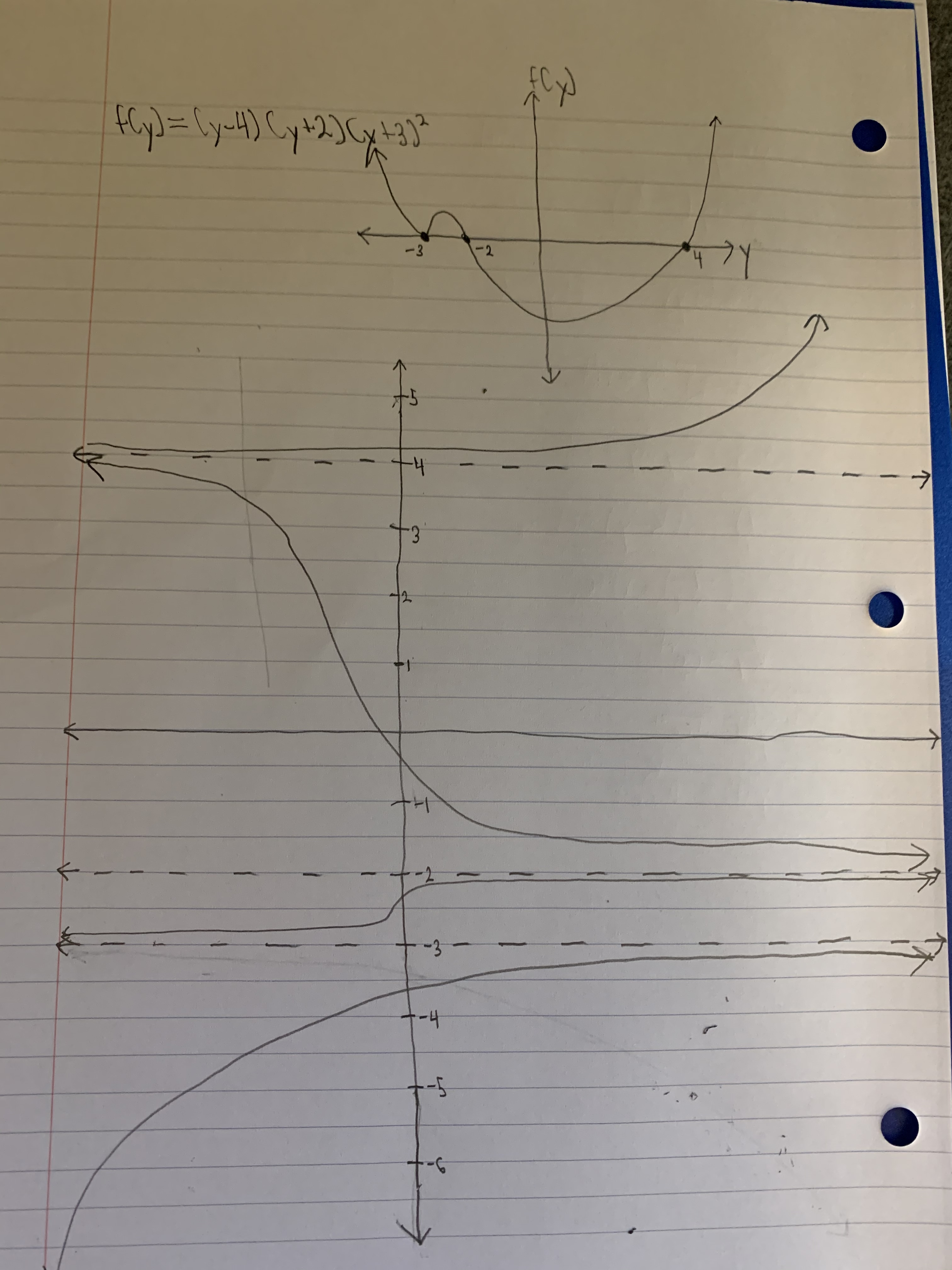
$$ f(y)=(y−4)(y+2)(y+3)^2 $$
The equilibrium solutions of this equation are $$ y= -2, -3, 4 $$
My autonomous equation I received was:
$$f(y) = - (y-3)(y+1)(y+2)^{2}$$
My equilibrium solutions are:
$$ y=-2,-1,3 $$
The equation I received was
$$f(y) = -(y - 4)^2(y - 3)(y - 2)$$
The equilibrium solutions are $y = 2, 3, 4$
Sketch of $f(y)$ with roots:
Sketch of equilibria and other solutions:
The autonomous equation I received was
$f(y) = -(y-4)(y-1)^2(y+2)$
The equilibrium solutions are
$y = -2,1,4$
The autonomous equation I received was
$$f(y) = -(y+2)(y+3)(y+4)^2$$
The equilibrium solutions are $$y=-2,-3,-4$$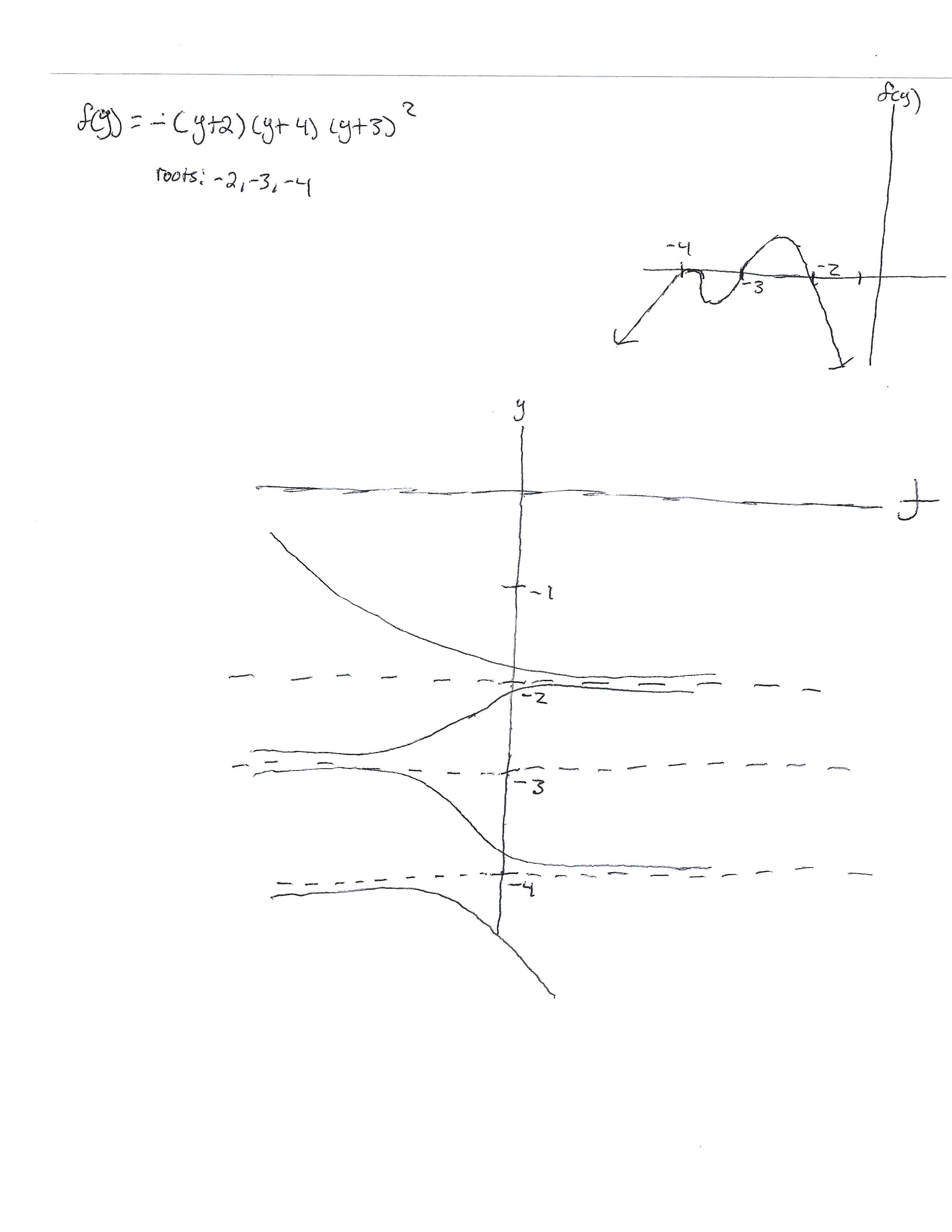
The autonomous equation I received was:
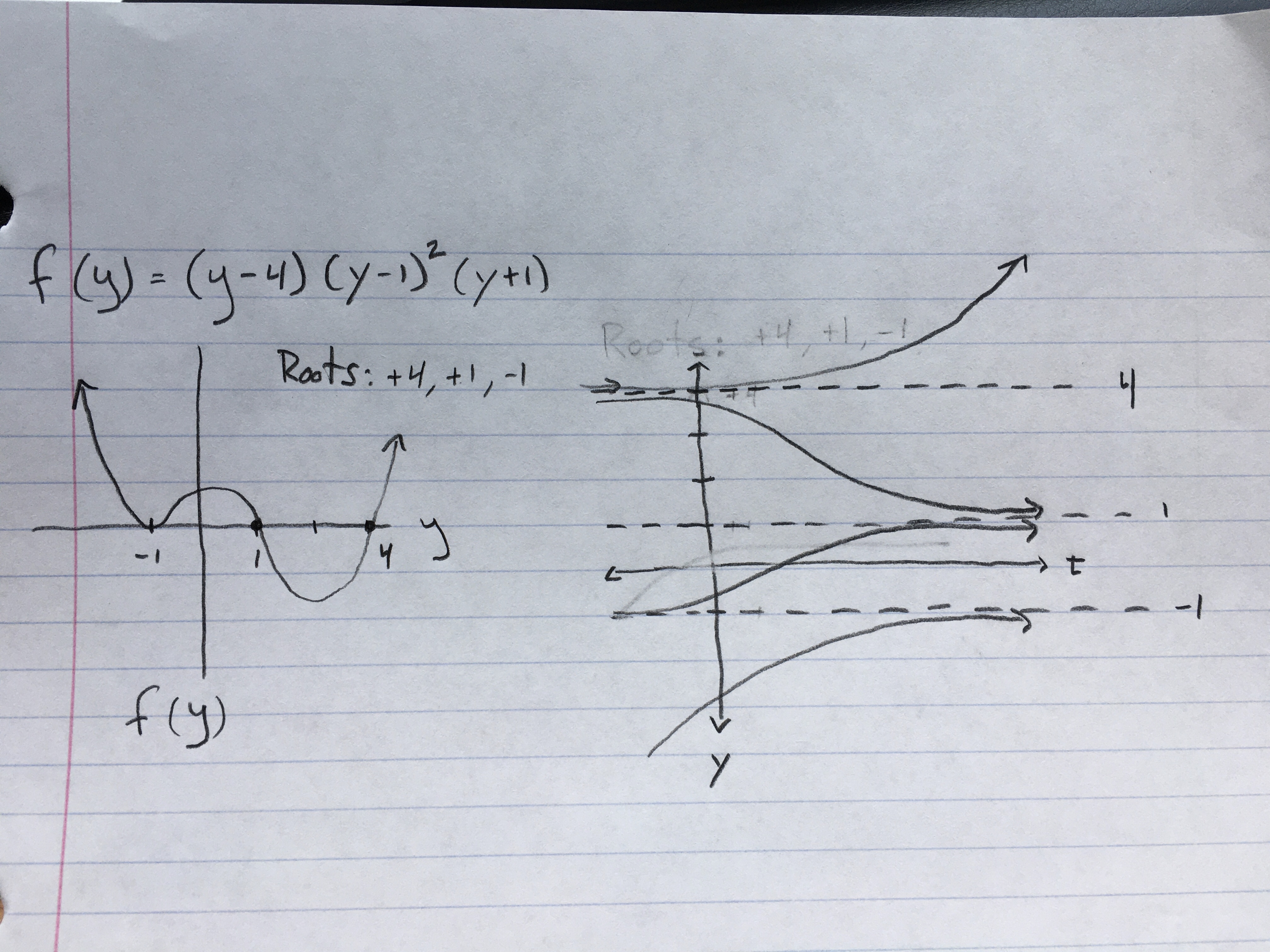
$$f(y)=(y-4)(y-1)^2 (y+1)$$
With equilibrium solutions:
$$-1,+1,+4$$
The equation I was given was: $$f(y) = y^2(y+1)(y+4)$$
The equilibrium solutions are: $$y = 0, y = -1, y = -4$$
The function I was given was $$f(x)=(y-4)(y-2)^2(y+4).$$ The solutions are y=-4,2,4 , where multiplicity at 2.
The Equation I got was:
$$ f(y)=−(y−4)y^2(y+3) $$
The equation I had was
$$f(y)=(y-4)(y-1)(y+1)^2$$
Equilibrium solutions are
$$y=4,y=1,y=-1$$
The autonomous equation I received was: $$f(y)= -(y-3)(y-2)(y+1)^2$$
The equilibrium solutions for this equation are: $$y= -1,2,3$$
With a multiplicity of 2 at $$y=-1$$
My equation was:
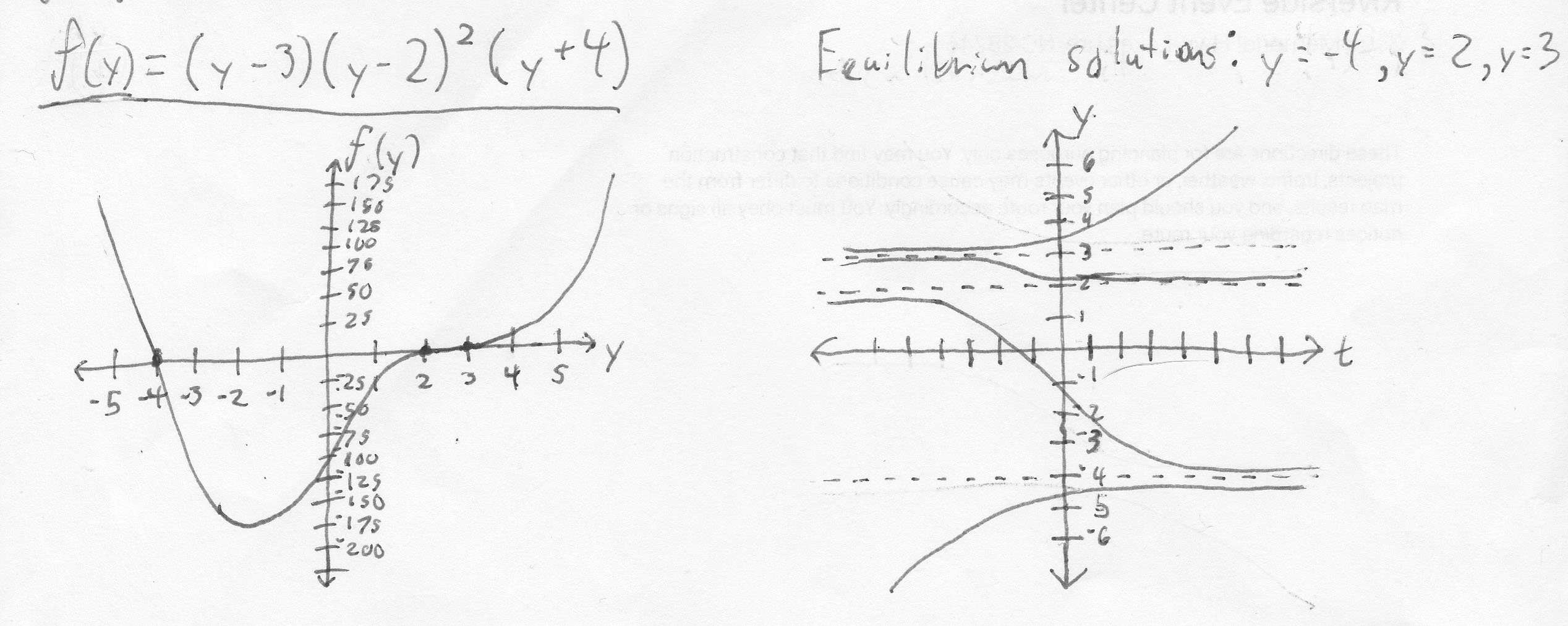
$$f(y) = (y-3)(y-2)^2(y+4)$$
Equilibrium solutions are:
$$y = -4, y = 2, y = 3$$
My equation is
$$f(y)=(y-4)^2(y-1)(y+3)$$
My equilibrium solutions are
$$y=4, 1, -3$$
With multiplicity 2 at
$$y=4$$
Equation:
$f(y)=(y-2)(y-1)(y+1)^2$
Equilibrium Solutions:
y = -1, 1, 2
My equation was: $f(y)=-(y-2)^2y(y+1)$
With solutions of $y=-1, y=0,$ and $y=2$ with multiplicity at 2.
The equation I got was $f(y)=-y(y+3)(y+4)^2$ , and it has equilibria at $y=-4,-3,0$
@Wiggenout
Try to insert a PNG, rather than attaching a PDF.