Eigen-Ranking

Let's start the semester with a pretty cool demonstration - we'll use pure linear algebra to rank an athletic conference. While the specific example we'll look at involves Big Ten's College football (it is my class, after all), the idea is really much more broadly applicable. The technique we'll use, in fact, is essentially Google's Page Rank.

The situation

Our objective is to rank the Big Ten College Football season using the results of last year's The image shown below illustrates the 2018 Big Ten College Football season.

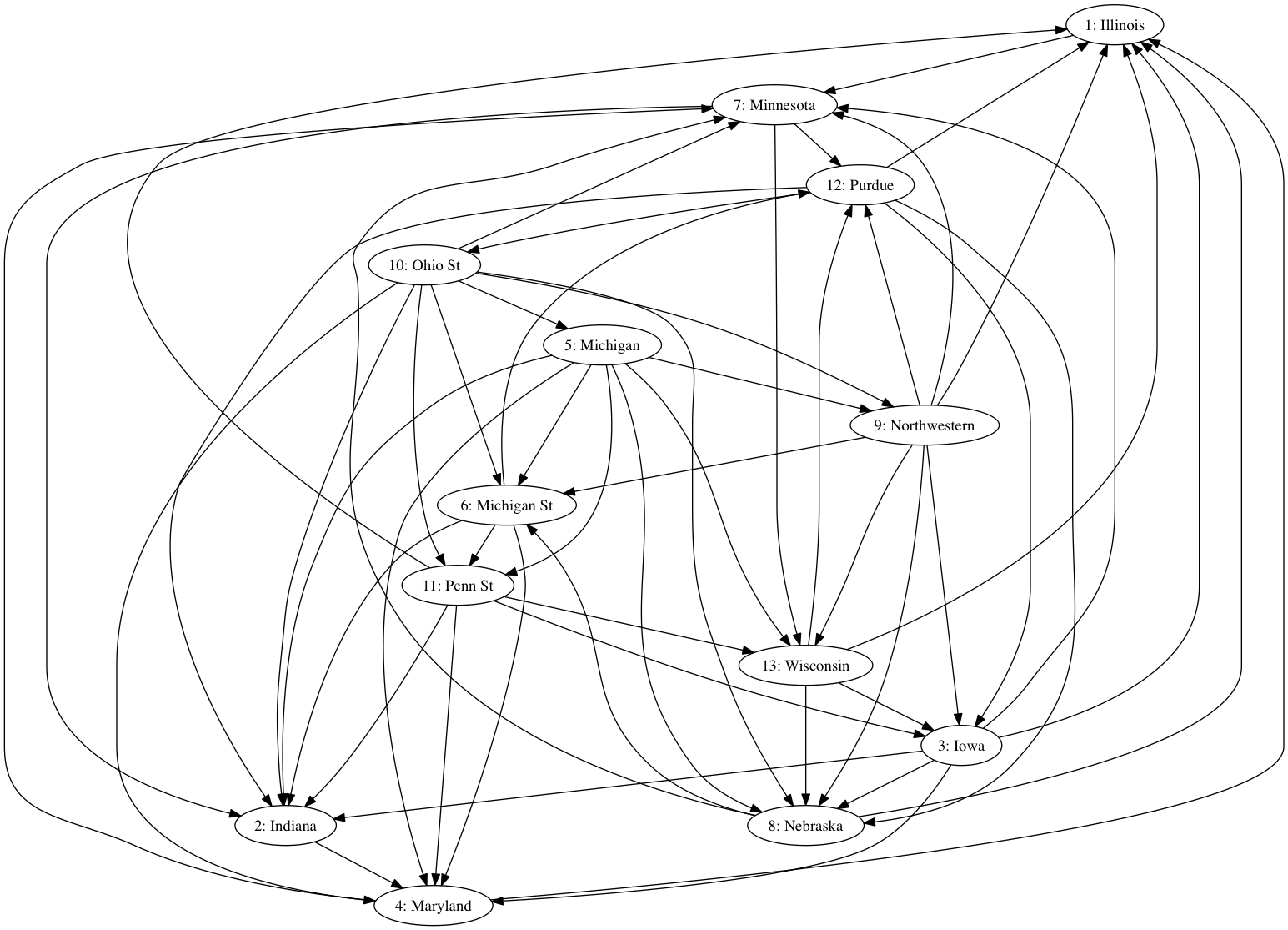
This type of image is called a directed graph. The circled nodes correspond to teams as follows:

Illinois
Indiana
Iowa
Maryland
Michigan
Michigan St
Minnesota
Nebraska
Northwestern
Ohio St
Penn St
Purdue
Wisconsin

If team i defeated team j, then we draw a directed edge from i to j. Ohio St, for example, beat Michigan; thus, there is an edge from node 10 to node 5.

Strangely, the Big Ten has 14 teams. The list above includes all those teams but Rutgers, which was winless in the Big Ten last year.

Matrix Formulation

The information incorporated in the directed graph can be encapsulated in an important construct for linear algebra called a matrix, which is essentially just a rectangular arrangement of numbers. The matrix for our directed graph looks like so:

\[ \left(\begin{array}{rrrrrrrrrrrrr} 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \end{array}\right) \]

The order of the rows and columns of this matrix correspond exactly to the order of teams in our list. Thus, the entry in row 10 and column 11 is a 1 since Ohio St beat Michigan.

A little magic

Now we're going to perform some linear algebraic computations, using a mathematical software package called Sage, to rank the teams.

Just as I thought!

Comments

Don't feel that you should understand all this right away, particuarly the last portion. The example is meant to illustrate a fun application that we might understand down the road. Let's go ahead and try to isolate some important concepts right now, though.

Matrices (the plural of matrix) form one of the most important classes of objects that we'll study this semester. Much of of the first few weeks could be called matrix algebra, in fact.
Matrices can be used to model many things in applied mathematics. In the example above, we see how a matrix can be used to model an athletic teams results for a season. As we'll learn soon, they can also be used to model systems of equations.
Matrices can also be used to model many things in pure mathematics. We'll spend much of our semester exploring so-called linear transformations of vector spaces. Matrices can be used in exactly this context when the vector spaces are concrete Euclidean spaces.
Many of the computations in linear algebra are simple in principle, but cumbersome in practice. As a result, we will learn to use the computer a bit as a computational tool.
The fundamental computational magic in the code above occurs with the command M.eigenvectors_right(). Exactly what this does and why it works here will have to wait but eigenvalues, eigenvectors, and their applications will be the major topic of conversation near the end of the semester.
We like to work in the open.