Newton's method for Calc I

Newton's method is a technique to find numerical approximations to roots of functions. Given an initial guesss \(x_1\), Newton's method improves this guess by applying the function \[N(x) = x - \frac{f(x)}{f'(x)}.\] This produces \(x_2 = N(x_1)\). We then plug that back in to get \(x_3\) and continue. More generally, we produce a sequence \((x_k)\) via \(x_k=N(x_{k-1})\).

Example

Let \(f(x) = x^3-x-1\). It's evident from a graph that there's one root.

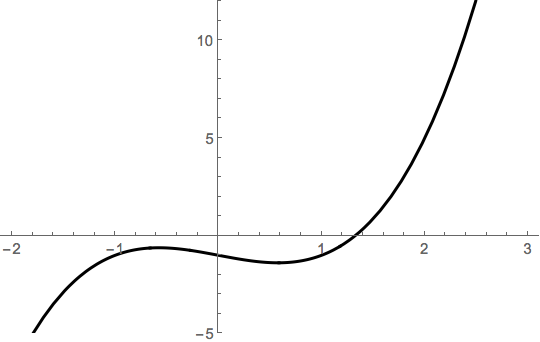
Newton's method works by riding the tangent line from an initial guess. If we note that \(x_1=2\) is pretty close to the root, we compute \(x_2 = N(x_2)\), where \[N(x) = x - \frac{f(x)}{f'(x)} = x - \frac{x^3-x-1}{3x^2-1}.\] Thus, \(x_2 = N(2) = 2-5/11 \approx 1.54545\). Geometrically, this point is obtained by riding the tangent line to the \(x\)-axis:

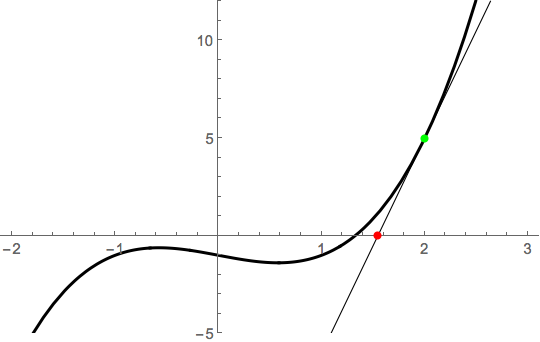
If we do that again, we end up even closer to the root:

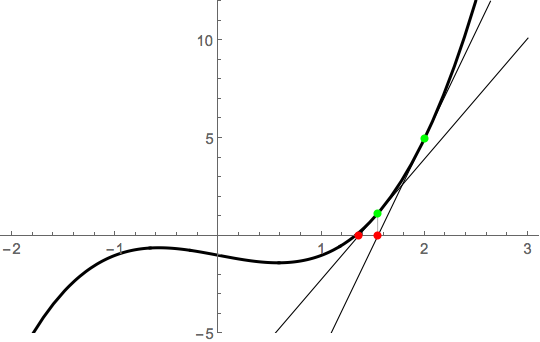
That's why we iterate!

Resources for Newton's method and solving equations

Solving equations

• Desmos: Just plot two sides of an equation together and click on the intersection point to get the solution, like this.
• WolframAlpha: Just type in your equation, like this.
• Sage: More of a programming tool, which you can use like like this.

Performing Newton's method

To actually perform several Newton iterates, it makes sense to use a programming tool. You can do it with Sage like this.

Exercises

1. Use a numerical tool to solve the following equations. Be sure to find all solutions
   1. \(x^5-x-1 = 0\)
   2. \(x^5-2x-1 = 0\)
   3. \(\sin(3x) = x/2\)
2. For each of the following functons, take three Newton steps from the given initial point
   1. \(f(x) = x^2 - 2\) from \(x_1 = 2.0\)
   2. \(f(x) = \sin(x)\) from \(x_1 = 3.0\)
   3. \(f(x) = x^5-x-1\) from \(x_1 = 1.0\)
3. The equation \(\sin(x)=x/9\) has 7 solutions. We want to find an approximation to the largest solution. Use a graph to find a good initial approximation for your \(x_1\) and apply Newton's method from that point obtain the approximation.