We are continuing with our study of the iteration of functions of the form \[f_c(z) = z^2 + c.\] We've already developed a knowledge of this thing called the Julia set, which lives a complex dynamical plane. That is, we fix a complex number \(c\) and we study the iteration of the function \(f_c\). The Julia set is a picture of where the chaos lies for this type of function.
The Mandelbrot set, by contrast, lives in a complex parameter plane. That is, for various choices of the complex parameter \(c\), we ask what is the structure of the corresponding Julia set for \(f_c\)? As it turns out, the orbit of the critical point \(z_0=0\) tells us a lot about the structure of the Julia set.
Theorem: Let \(f_c(z)=z^2+c\). There are two, mutually exclusive possibilities for the orbit of \(z_0=0\) under iteration of \(f_c\), which lead to two different types of Julia sets:
Definition: The Mandelbrot set is the set of all \(c\) values such that the Julia set of \(f_c(z)=z^2+c\) is connected or, equivalently, the set of all \(c\) values such that the orbit of \(z_0=0\) under iteration of \(f_c\) stays bounded.
Thus, the Mandelbrot set is a coarse partition of the parameter plane into two regions corresponding to two very different types of Julia set. The crazy thing though, is that the Mandelbrot has a number of different components - each of which corresponds to a type of Julia sets. Thus, we get for free a much finer classification of Julia set behavior than we were looking for. The main point behind our Julia sets and the Mandelbrot set demo, is to play with this correspondence.
If you play with our tool for creating cobweb plots and set the example to "Quadratic", you should notice a period doubling cascade and ensuing chaos as \(c\) decreases toward \(-2\). In fact, we can generate a bifurcation diagram for the quadratic family, just as we did for the logistic family. If we plot this together with the Mandelbrot set, an amazing correspondence arises:
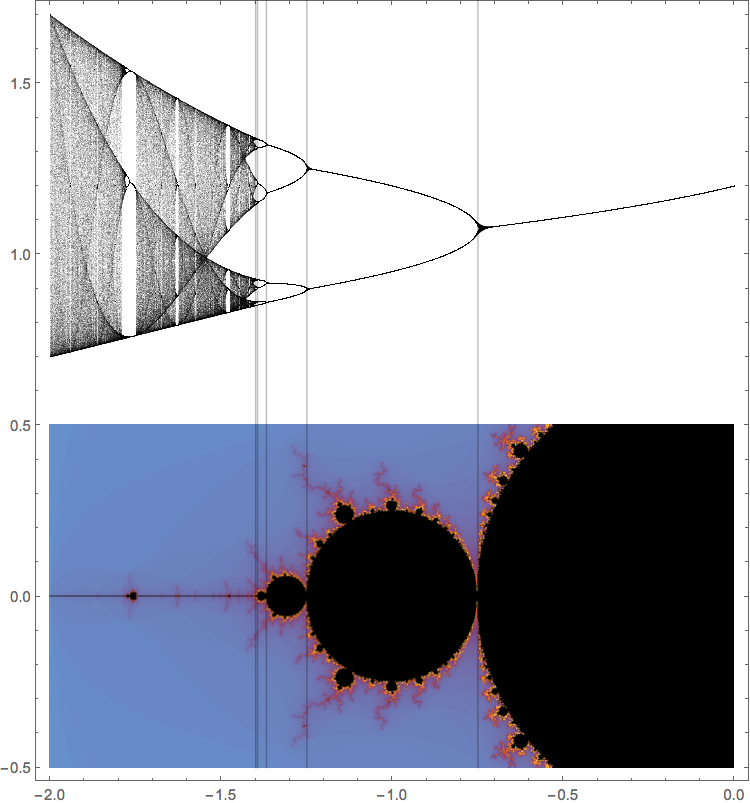
The image above was lifted from this stackexchange post. That's just one of many entertaining and informative posts.