Solving and interpreting equations is absolutely central in mathematics. Some simple examples include
If you've taken at least a pre-calculus class, you can probably find solutions for at least the first 4 of these:
While simple, these equations are chosen to illustrate a point. Even though each equation involves simple arithmetic operations with an unknown symbol \(x\) and the natural numbers, the solutions in more and more complicated sets of numbers. Specifically, those solutions lie in
Each one of these three steps (the acceptance of negative and rational numbers and the realization that numbers like \(\sqrt{2}\) are irrational) was a huge step conceptually.
It seems reasonable to believe that a solution last equation \(x^2+1=0\) might exist in the appropriate number system, even though there is no real number that solves it. We call that system the set of complex numbers and denote it by \(\mathbb C\).
We begin by imagining that there \(x^2+1=0\) has some solution; we denote that solution by the symbol \(i\). We also suppose that \(i\) has all the arithmetic properties we expect a number to have. That is, we can add it to itself or any other number to get the sum of those numbers. The addition has to be commutative and the same should go for multiplication. All of a sudden we've got lot's more numbers like \(2i\) and \(2+3i\) and lots more. We can do arithmetic with \(i\) just as we would with any other symbolic constant; we just have to occasionally account for the fact that \(i^2=-1\). For example:
\[ (1+2i) + (3+4i) = 4+6i \]and
\[\begin{align} (1+2i) (3+4i) &= 3+8i^2 + 4i+6i \\ &= (3-5) + (4+6)i \\ &= -2+10i. \end{align}\]In short, we can define a function using arithmetic operations and then operate on the complex numbers as usual. In complex variables, it is common to denote the variable of the function by \(z\). For example, we might define a function by \(f(z)=z^2 + (3-2i)\). Then, we could apply \(f\) to a complex number like \(1+3i\). Then we'd get
\[\begin{align} f(1+3i) &= (1+3i)^2 + (3-2i) \\ &= ((1-9) + 6i) + (3-2i) = -5+4i. \end{align}\]Since we can define functions of complex variables, we'll be able to iterate them!
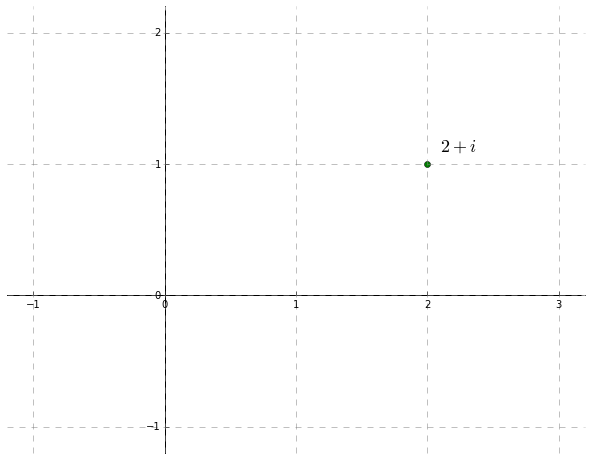
Just as real numbers can be visualized on a number line, complex numbers can be visualized on a plane. The complex number \(a+bi\) simply corresponds to the point \((a,b)\). For example, here's a plot of the number \(2+i\):

Complex addition can be viewed as displacement. This is very similar to how we view addition of vectors. For example, here's a look at \((1+2i) + (3+i)\):
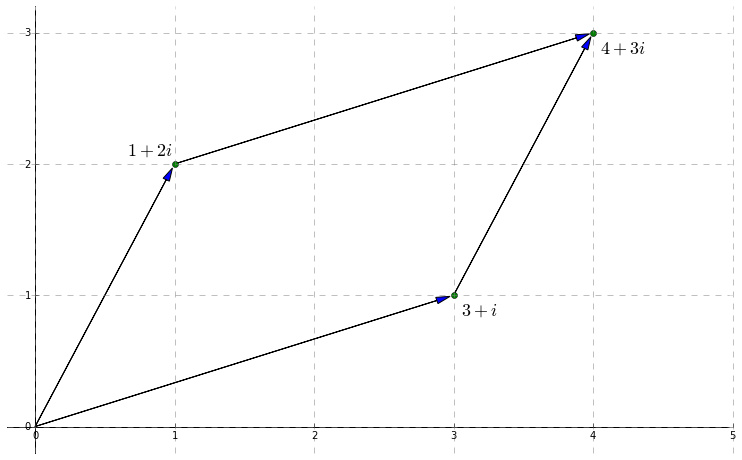
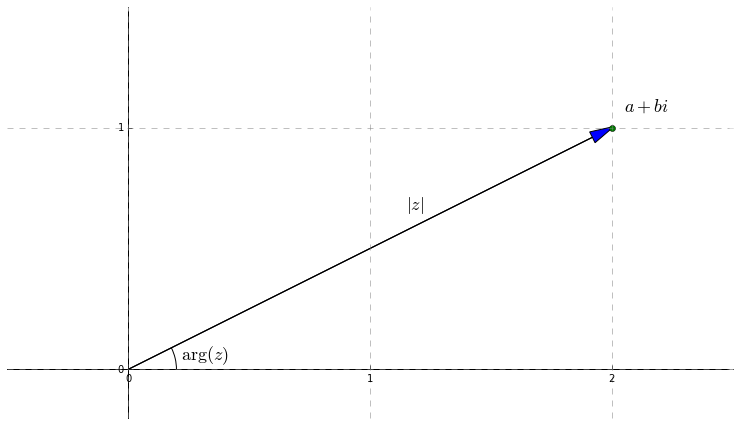
In this picture, the sum itself \(4+3i\) can be viewed as the diagonal of the parallelogram. This illustrates a very important inequality known as the triangle inequality. Given a complex number \(z\), we define its absolute value \(|z|\) to be the distance from \(z\) to the origin. The triangle inequality relates the absolute values of two complex numbers \(w\) and \(z\) to the absolute value of their sum. Specifically:
\[|w+z| \leq |w|+|z|.\]All this really says is that one side of a triangle is less than the sum of the other two sides.
Though it's less immediately evident, complex multiplication also has a nice geometric interpretation. Given a complex number \(z\), we define its its argument \(\arg(z)\) to be the angle an observer at the origin must rotate from the positive real axis to look right at \(z\).
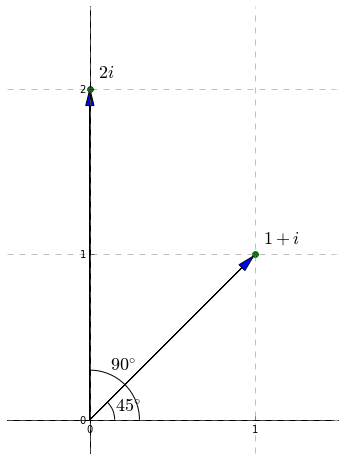
Now, when we multiply two complex numbers, their absolute values multiply and their arguments add. For example, if \(z_1=1+i\) and \(z_2=i\), then \[z_1\times z_2=(1+i)i=i+i^2=i-1.\] The absolute values of the first two are \(\sqrt{2}\) and \(1\); the absolute value of their product is \(1\times\sqrt{2}=\sqrt{2}\). The arguments of the first two are \(45^{\circ}\) and \(90^{\circ}\). The argument of their product is \(135^{\circ}\).
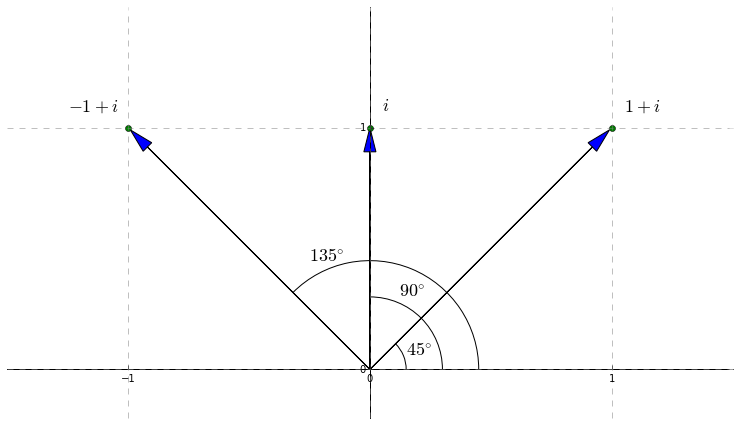
As a result, if we square a complex number, its absolute value squares and its argument doubles. For example, if \(z=1+i\), then \[\begin{align} z^2 &= (1+i)^2 = 1^2+i^2 + 2i \\ &= 1-1 + 2i = 2i \end{align}\] Note that the absolute value of \(z\) is \(\sqrt{2}\) and its argument is \(45^{\circ}\). The absolute value of \(z^2\) is \(2\) and its argument is \(90^{\circ}\).