Iteration of a single function on the complex plane (which gives rise to a Julia set) and the IFS technique (to generate self-similar sets) seem very different. But it's hard to notice as you zoom into a Julia set that the same patterns seem to repeat over and over. Just have a look at this youtube video or this one. Let's try to understand why.
Recall that the Julia set is where the chaos lives when we iterate a function \(f:\mathbb C \to \mathbb C\). Its complement (the Fatou set) is the stable set of the function. As a result, when we iterate \(f\) from a point near the Julia set, the iterates tend to move away from the Julia set and into the Fatou set. You can see this quite clearly for the function \(f(z)=z^2\) by playing with our complex squaring function demo or for functions of the form \(f_c(z)=z^2+c\) by playing with our Julia sets and the Mandelbrot set demo.
Again, the main observation is that the Julia set of \(f\) is a dynamical repellor of \(f\).
Now, if the Julia set of \(f\) is a dynamical repellor of \(f\), it makes sense that the Julia set should be a dynamical attractor for the inverse function \(f^{-1}\). But a function can have several inverses. This yields something like an iterated function system for the Julia set.
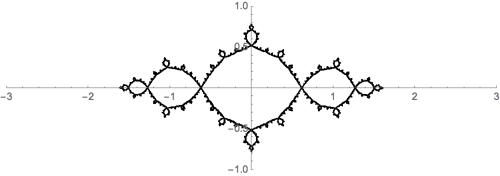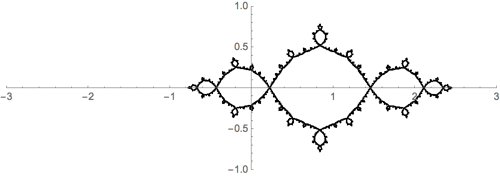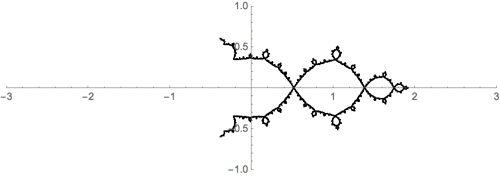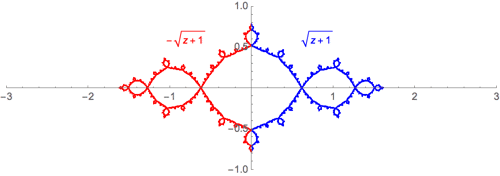
Let's take the squaring family \(f_c(z)=z^2+c\), for example. It's not hard to solve \[w=z^2+c\] for \(z\) to get \(z=\pm\sqrt{w-c}\). This yields two inverse functions \[f^{-1}(z) = \pm\sqrt{w-c}.\] Thus, we expect the Julia set, \(J\) to satisfy an IFS like equation: \[J = \sqrt{J-c} \, \bigcup \, -\sqrt{J-c}.\] I guess it's not exact self-similarity, since the square root function isn't a similarity tranformation - but, it should look close.
Here's an illustration for \(f(z)=z^2-1\):

All this yields another method to generate images of Julia sets - we simply apply the deterministic or random algorithm for generating IFS images to the list of inverses of the function. That's exactly what's going on in our Julia sets and the Mandelbrot set demo when you choose the inverse iteration algorithm.