Iterated function systems

Images of self-similar sets can be generated using a tool called and iterated function system or IFS, which is just a list of the functions that scale the whole set onto the smaller pieces. The purpose of this page is to explain the language of iterated function systems just well enough so that we can play with our IFS Visualizer.

Types of functions

We're going to look at examples of iterated function systems that act on two dimensional space - i.e. the plane. Thus, they'll generate images in the plane, rather than in 3D space like this. First, we need a bit to know what kinds of functions an IFS can contain.

• Given two points in the plane, \(x\) and \(y\), the distance between them is denoted by \(d(x,y)\).
• A similarity is a function \(f\) with the property that \(d(f(x),f(y))=r\,d(x,y)\) for all points \(x\) and \(y\), where \(r\) is just some positive number.
• When \(r<1\), the similarity is called contractive.

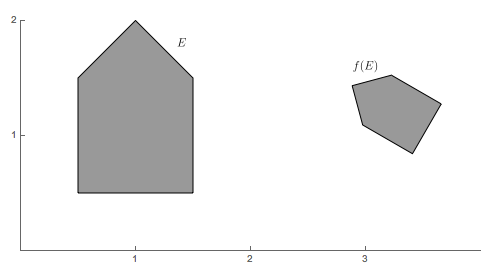
The simplest type of iterated function system is simply a list of contractive similarities. The important fact about a similarity (sometimes called a similarity transformation) is that the image of a set under a similarity is a geometrically similar figure. A generic illustration of this is shown below.

Similarity transformations can be built out of a few types of simple tranformations.

• A shift simply shifts a point by adding another point (or vector, if you prefer).
  • The IFS Visualizer represents the shift through the direction \(d\) by shift(d).
• A rotation simply rotates about a point through an angle.
  • The IFS Visualizer represents the rotation that rotates through the angle \(t\) about the point \(x_0\) by rotate(t,x0). If the point \(x_0\) is not present, it is assumed to be the origin. Note that \(t\) represents radian measure. The IFS Visualizer knows the multiplicative constant degree so that you can type 90*degree or pi/2 to represent a right angle.
• A scaling transformation simply contracts or dilates by the same factor in all directions about some fixed point in the plane.
  • The IFS Visualizer represents the scaling transformation that scales about the point \(x_0\) by the factor \(r\) by scale(r,x0). If the point \(x_0\) is not present, it is assumed to be the origin.
• A reflection simply reflects about a line..
  • The IFS Visualizer represents a reflection about the line containing the point \(x_0\) and with normal vector \(n\) by reflect(n,x0). If the point \(x_0\) is not present, it is assumed to be the origin.
    Note that the term normal is a synonym for perpendicular in this context.

Finally, similarity transformations can be composed with one another to form more complicated transformations. In the IFS Visualizer, this is accomplished with the compose method. Thus, the following bit of code defines a function that says

1. Rotate 60 degrees, then
2. scale by the factor \(1/3\), then
3. shift to the right a distance of \(1/3\).

shift([1/3,0]).compose(scale(1/3)).compose(rotate(60*degree))

At this point, you should have a good look at the IFS Visualizer and try to figure out the function defintion box in the upper left of the application.

Iterating an IFS to generate a self-similar set