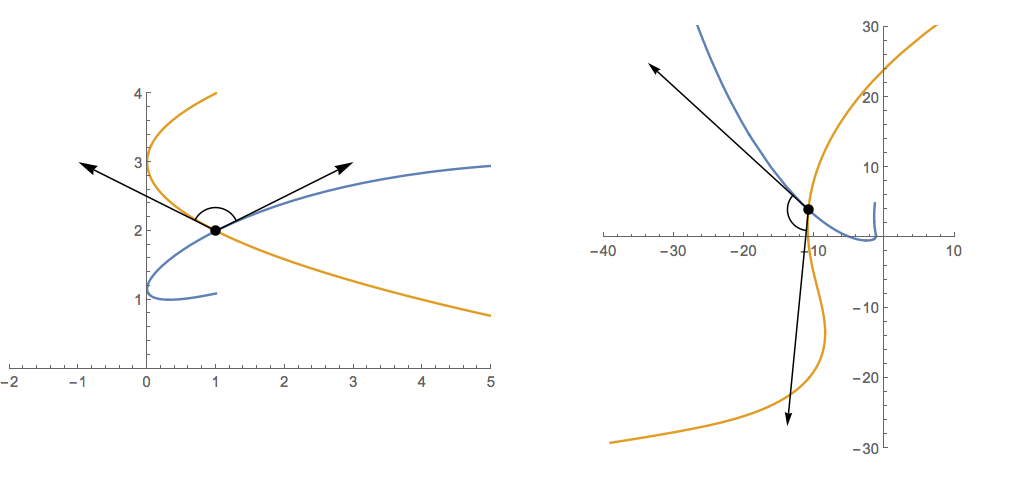
On the left side of the figure below, we see the two paths
\[\begin{align} \gamma_1(t) &= (t^2+2t+1)+(\sin(t)+2)i \\ \gamma_2(t) &= (t^2-2t+1)+(t+2)i \\ \end{align}\]The paths are pretty much arbitrary, except that \(\gamma_1(0)=\gamma_2(0)=1+2i\). On the right, we apply the (almost completely arbitrary) function \(f(z)=z^3+z^2+\sin (z)\). The angle between the paths where they cross should be preserved.
