Visualizing the Takagi function

Recall the Takagi function $\tau$ that we discussed in class - it was defined as follows: We first defined $\varphi(x)=|x|$ for $-1/2\leq x \leq 1/2$ and extended $\varphi$ to periodic. This creates a basic sawtooth wave. We then defined $\tau$ in terms of $\varphi$ by
$$\tau(x) = \sum_{n=0}^\infty \frac{1}{2^n}\varphi(2^n x).$$

We can plot this thing, along with the line $y=x$ quite easily:

phi[x_] := With[{y = Mod[x, 1]},
  If[y <= 1/2, y, 1 - y]];
tau[x_Real] := Sum[phi[2^k*x]/2^k, {k, 0, 53}];
Plot[{tau[x], x}, {x, 0, 1}, PlotRange -> {0, 0.75}]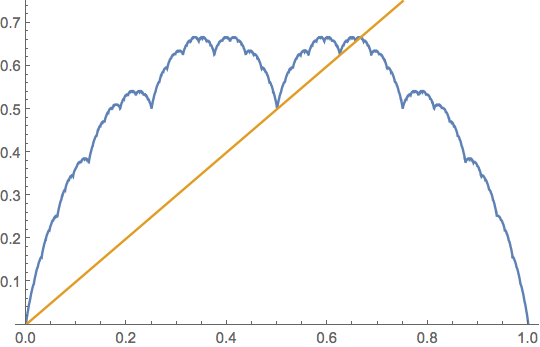

Note that it appears that the graphs intersect at the cusps where $x=1/2$, $x=3/4$ and more. Those are fixed points of $\tau$.

Do you think there would be a semi-simplistic way to investigate any cyclic behavior in the Takagi function as pertains to iteration?

Well, one thing you can do is just experiment. Once you've got a computer program that's computes values of the function, you can have it iterate from a number of different starting points to see what sorts of behaviors are possible.

So maybe I am completely off base here, but is there a way to turn the Mathematica code up top into a pure function all the cobweb plot code I have found requires a way to pass things through the function?

I think I might just be beating my head against a wall.

@Ricky_Bobby Don't go overboard just yet - this is a research level problem, remember!

That said, I'll mention two things.

1. Once you have a function f defined in Mathematica, you can iterate it $n$ times starting from $x_0$ by executing:

   NestList[f,x0,n]

2. I taught a class in Chaos back in 2013. There's a bunch of Mathematica notebooks on the webpage for that class.