Plotting challenges

We've got some pretty crazy functions in our real analysis class and we're trying to develop some mad plotting skills in our numerical analysis class. Why don't we try to mesh these together? So this question is in the new Analysis category, which is open to both my analysis classes. Here are a few fun functions to try:

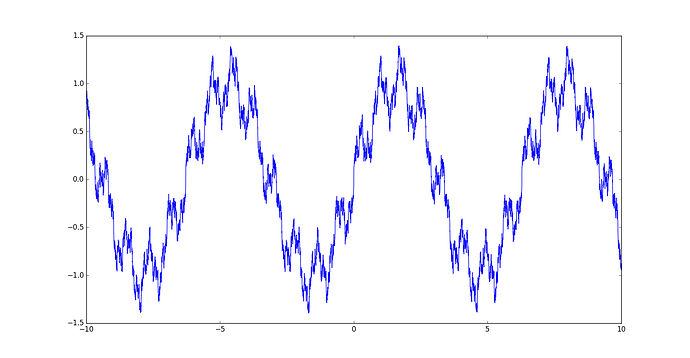
1. $\displaystyle f(x) = \sum_{k=1}^{\infty} \sin(k^3x)/k^2$

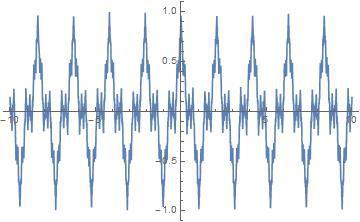
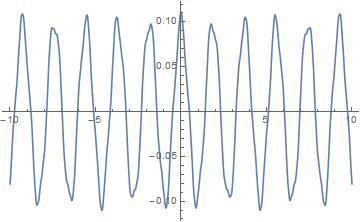
2. $\displaystyle f(x) = \sum_{n=0}^{\infty} a^n \cos(b^nx)$
   For this one, you might try several choices of $a$ and $b$. Be sure to consider the cases, $1< 1/a < b$ and $1 < b < 1/a$.
   

3. Let $\{r_1,r_2,\ldots\}$ be an enumeration of the rational numbers. For each $r_n$, define
   $$u_n = \begin{cases}
   1/2^n & \text{ for } x>r_n \\
   0 & \text{ for } x\leq r_n
   \end{cases}$$
   and then let
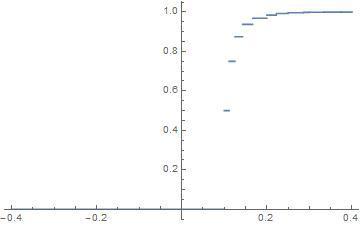
   $$h(x) = \sum_{n=1}^{\infty} u_n(x).$$
   Plot $h(x)$.
   
   
   
   
   
   
   

Any plotting tool of your choice is acceptable but plots produced by Python or Mathematica are particularly of interest.

Had to do a a little research, but here is what I came up with for the first one.

n = 100
def f(x):
    return sum([np.sin(k**3*x)/(k**2) for k in range (1,n)])

xs = np.linspace(-10, 10, 1000)
plt.plot(xs, f(xs))

figure_1.png1638x852 80.7 KB

Here are some cool examples of number 2. I used Mathematica to expedite the process.

Here is

$$\sum_0^{500} \left(\frac{1}{2}\right)^n\cos(3^n x)$$

 Plot[Sum[.5^n Cos[3^n*x], {n, 1, 500}], {x, -10, 10}]

"This is how a spider monkey does math."-me

@Ricky_Bobby Very cool! I edited my question a bit to reflect better choices of $a$ and $b$. I see that you figured out a good one on your own and I deleted the other two that are actually divergent.

Here is my go at number 3. Also this is in Mathematica.

l = Sort[DeleteDuplicates[
Flatten[Table[Table[{x/y}, {x, 1, 10}], {y, 1,    10}]]]]
g[x_, n_] := Piecewise[{{(1/2^n), x >= l[[n]]}, {0, x <= l[[n]]}}]
Plot[Sum[g[x, n], {n, 1, 15}], {x, -.4, .4}]

Here is another way I tried to do part 2 using the manipulate command in Mathematica. The picture is similar but the code gives you sliders to play with the two parameters.

Manipulate[
Plot[Sum[a^n Cos[b^n*x], {n, 1, 500}], {x, -10, 10}], {{a, .1, 
"Outside parameter"}, .1, 5}, {{b, .1, "Inside parameter"}, .1, 5}]

@Ricky_Bobby Whoa!!!!!!!!!!!!!!!!!!!!!!!!!