Convergence of a Taylor series

Prove that the Taylor series of $\sin(x)$ actually converges to $\sin(x)$.

Here is a shot at it!

and we want to show that in fact

$$\sin(x)= \sum_{N=0}^{\infty}\frac{1^{-1}}{(2N+1)!}x^{2N+1}$$

We can start by applying the Legrange's Remainder Theorem. Then because $\sin(x)$ is infinitley differentiable on $(-\mathbb{R},\mathbb{R})$ and $$a_n=\frac{f^n(0)}{n!}$$. Then we know for $x\neq0$ there exists a c such that $|c|<|x|$ where the error function is equal too.

$$E_N(x)=\frac{f^{N+1}(c)}{(N+1)!}x^{N+1}$$
Thus we can see that for all derivatives of $\sin(x)$ that $$|\sin^{N+1}(x)|\leq1$$ for all N.

Then we can see

$$|E_N(x)|=|\frac{f^{N+1}(c)}{(N+1)!}x^{N+1}|\leq|\frac{1(x^{N+1})}{(N+1)!}|\rightarrow0$$

Thus

$$\sin(x)= \sum_{N=0}^{\infty}\frac{1^{-1}}{(2N+1)!}x^{2N+1}$$

Also some cool Mathematica code showing a Taylor series approximation graphed out to n=15 and then an overlay onto $\sin(x)$.

Graph of $\sin(x)$

a = Plot[Sin[x], {x, -5 Pi, 5 Pi}]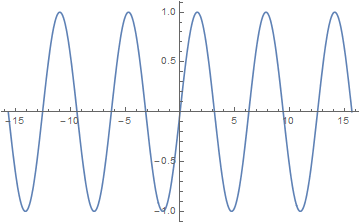

Graph of $$\sum_{N=0}^{15}\frac{1^{-1}}{(2N+1)!}x^{2N+1}$$

Plot[Expand[
  Sum[((-1)^k/(2*k + 1)!)*x^(2*k + 1), {k, 0, 15}]], 
  {x, -5*Pi, 5*Pi}, PlotStyle -> Red]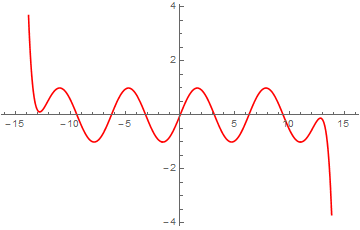

The the graph of the overlay

Show[a, b]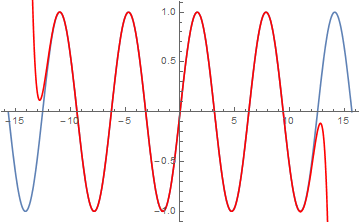

This looks pretty cool! One question; your second line of Mathematica code has a lot of unfamiliar stuff in it. Did you type it in that way or is it just the Mathematica typesetting going crazy?

Typesetting stuff to get the cool $\sum$.

@Cromer @Ricky_Bobby Yeah, so if you copy and paste that, it actually appears as typeset input in Mathematica. I guess I prefer Mathematica's so called InputForm here and edited the post accordingly. It's really easy to go back and forth, though. If groovyTypesetExpr is a Mathematica expression containing groovy typeset stuff and you want the boring linear expression, just do

groovyTypesetExpr // Hold // InputForm

and copy the part inside the resulting Hold. Conversely, if you want boringLinearExpression in it's groovy typeset form, just do

boringLinearExpression // Hold // StandardForm