A Fourier series

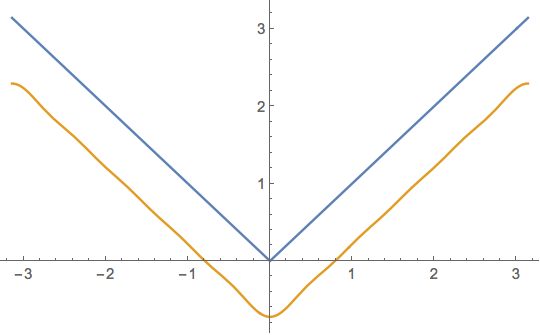
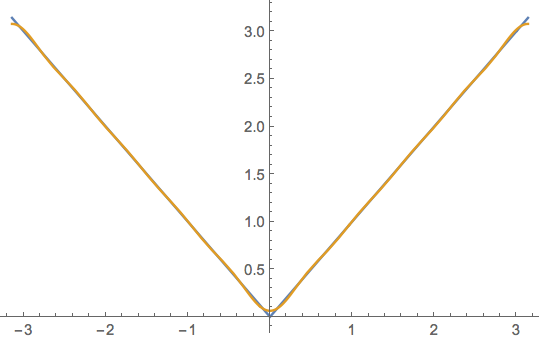
So, who's going to try to compute the Fourier series of $f(x)=|x|$?

I'll get you started! You want to find coefficients $a_n$ and $b_n$ so that
$$|x| = \frac{1}{2}a_0 + \sum_{n=1}^{\infty} \left(a_n\cos(nx) + b_n\sin(nx)\right).$$

Of course, we expect that the sine coefficients will zero because $|x|$ has even symmetry. You can prove this by multiplying through by $\sin(mx)$, integrating from $-\pi$ to $\pi$, and using the fact that the all but one integral that you see $(b_m\sin^2(mx)$ is manifestly zero. As a result, $b_m=0$ and, in fact, all $b_n$s are zero since $m$ was arbitrary.

Next, multiplying through by $\cos(mx)$ and using the orthogonality of the cosine/sine family, we see that
$$\int_{-\pi}^{\pi} |x|\cos(mx)dx = b_m \int_{-\pi}^{\pi} \cos^2(mx)dx.$$
Note that these integrals are easier if you integrate from $0$ to $\pi$ and multiply by $2$.

I am giving this a try and to pick up where @mark left off, due to orthoginality of cosine family, I can say
$$a_m \int_{-\pi}^{\pi} \cos^2(mx)dx = a_m \pi$$
So I then know that
$$a_m = \frac{1}{\pi} \int_{-\pi}^{\pi} |x| \cos(mx) dx$$

Then I am pretty sure I can go from zero to $\pi$, multipy by two and also lose the absolute value, giving me:
$$\frac{2}{\pi}\int_{0}^{\pi} x \cos(mx)dx$$
Then integrate by parts (it's been a while), let $f(x) = x, f'(x) = 1, g(x) = \frac{\sin(mx)}{m}, g'(x) = cos(mx)$ give me
$$\frac{2}{\pi}\Bigg[ \Bigg(\frac{x\sin(mx)}{m}\Bigg) \Bigg|_{0}^{\pi} - \int_{0}^{\pi}\frac{\sin(mx)}{m} dx\Bigg]$$

$$= \frac{2}{\pi m}\Bigg[ x\sin(mx) + \frac{\cos(mx)}{m} dx\Bigg]\Bigg|_{0}^{\pi}$$
$$ = \frac{2}{\pi m} \Bigg[ \Bigg( \pi \sin(\pi m ) + \frac{\cos(\pi m)}{m} \Bigg) - \Bigg ( 0 + \frac{\cos(0)}{m} \Bigg) \Bigg]$$
Since $\sin(\pi m) = 0$, $\cos(\pi m)$ is either $1$ or $-1$, and $\cos(0) = 1$, I get the following result:
$$ a_m = \frac{2}{\pi m} \Bigg( \frac{(-1)^n}{m} - \frac{1}{m} \Bigg) = \frac{2(-1)^n - 2}{\pi m^2}$$

Now, I am pretty sure I also have to consider $a_0$. So, $$a_0 = \frac{1}{2 \pi} \int_{-\pi}^{\pi} |x|dx$$ $$= \frac{1}{\pi} \int_{0}^{\pi} xdx$$ $$= \frac{1}{\pi} \Bigg( \frac{x^2}{2} \Bigg)\Bigg|_{0}^{\pi}$$ $$= \frac{1}{2\pi} (\pi^2 - 0) = \frac{\pi}{2}$$
If I am right, then putting it all together I get that:
$$f(x) = |x| = \frac{\pi}{4} + \sum\limits_{n=1}^\infty \Bigg( \frac{2(-1)^n - 2}{\pi n^2}\Bigg) \cos(nx)$$

@cseagrav I didn't check your computations at all; I simply generated a plot:

Plot[{Abs[x],
  Pi/4 + Sum[((2 (-1)^n - 2)/(Pi*n^2))*Cos[n*x], {n, 1, 10}]
 }, {x, -Pi, Pi}]

Something tells me that you're really close but your additive constant is off.

If, however, we follow the advice of @Professor.Membrane, and change the Pi/4 to a Pi/2, we get the following picture:

Maybe someone can see where I made the mistake. I am at work for the day but will try to troubleshoot during my lunch break. Hey @Ricky_Bobby!!! Didn't you say you already worked this problem? Help!

@cseagrav I think the issue is that

$$ a_{0} = \frac{2}{\pi}\int_{0}^{\pi} x dx = \frac{2}{\pi}\cdot\frac{\pi^{2}}{2} = \pi$$

So then we would have that

$$|x| = \frac{\pi}{2} + \sum_{n = 1}^{\infty} \left(\frac{2(-1)^{n} - 2}{\pi n^{2}}\right)\cos(nx)$$

Thanks @Professor.Membrane! Please help me figure something out. I have that $a_0 = \frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x)dx$. That is straight from the book, however when I research online and by your post which is obviously correct, I see $a_0 = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x)dx$. What am I missing?

Perhaps Abbott has the division by 2 in the definition of $a_0$ rather than in the definition of Fourier Series? Does that make sense to anyone but me?

I think the book says $$\frac{a_{0}}{2} = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(x) dx,$$ in which case you simply divided through by two twice (which would give you your original result of $$\frac{\pi}{4},$$ either that, or as you suggested, abbot defines $a_{0}$ as our $$\frac{a_{0}}{2}$$