Computational adventures in complex dynamics
A preliminary report
Complex dynamics as I saw it
- We study the iteration of $f:\mathbb C \to \mathbb C$
- We search for attractive regions computationally
- The complement is often interesting
- Exploration of examples is the fun part
Example: $\, f(z) = z^2$
Example: $\,f(z) = z^2-1$
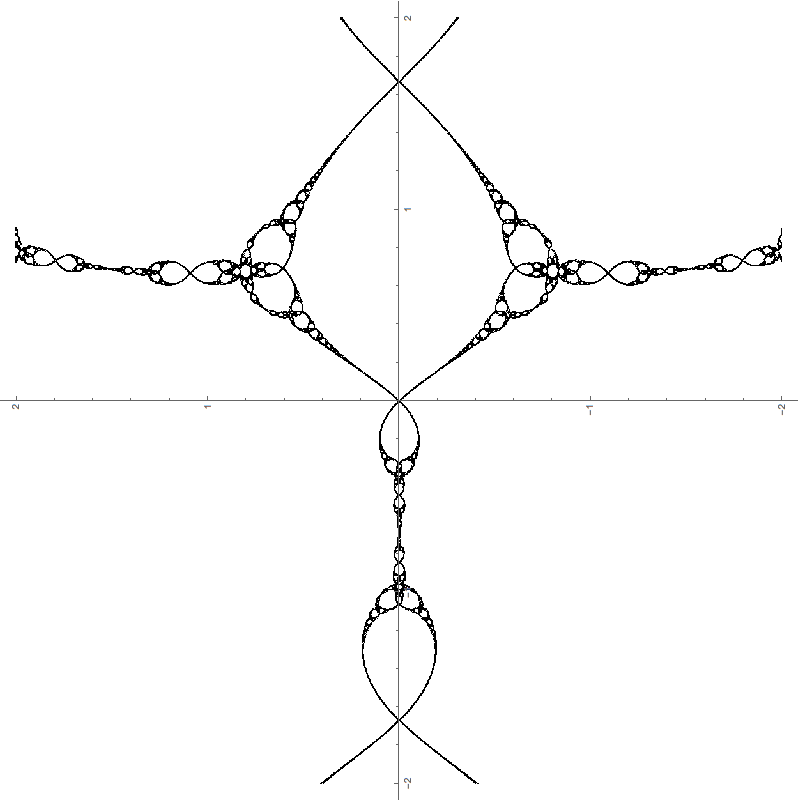
Inverse iteration 0
Inverse iteration -1
Weierstrass elliptic $\wp$ functions
A function $f:\mathbb C \to \mathbb C$ is elliptic if it is meromorphic and doubly periodic.
Given a lattice $\Lambda$ of periods, the associated Weierstrass elliptic $\wp$ function is $$\wp(z) = \frac{1}{z^2} + \sum_{\omega \in \Lambda \setminus \{0\}} \left(\frac{1}{(z-\omega)^2} - \frac{1}{\omega^2}\right).$$
Note that this is a parametrized family of functions and we often parametrize in terms of the Weierstrass invariants $g_2$ and $g_3$ that relate to $\wp$ via the differential equation $$(\wp'(z))^2 = 4(\wp(z))^3 - g_2 \wp(z) - g_3.$$
An image lifted from a 2002 paper of Hawkins and Koss
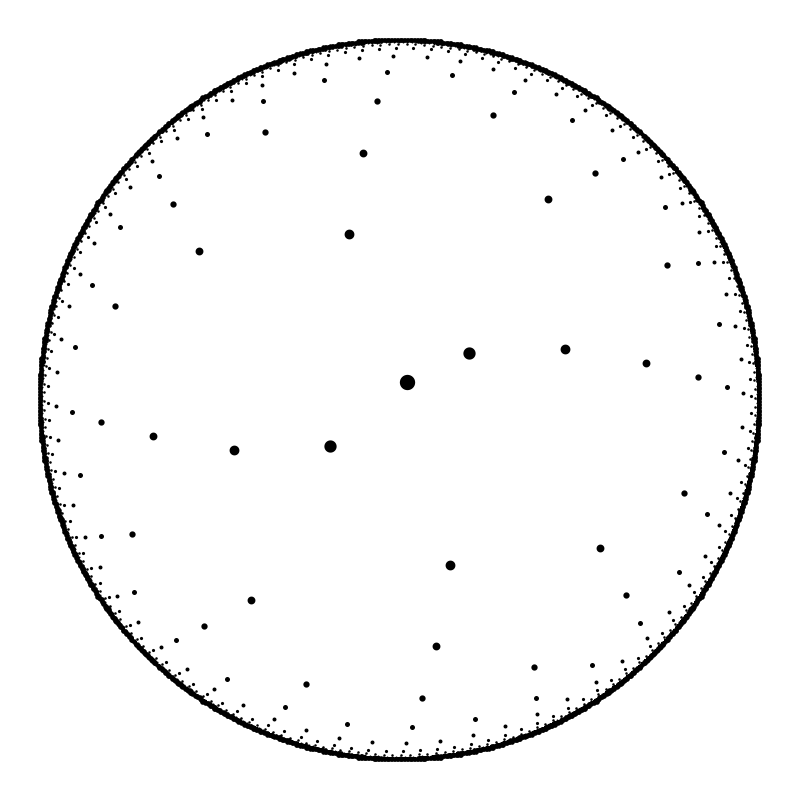
My first attempt at inverse iteration using just $$\pm \wp^{-1}(z;g_2,g_3).$$
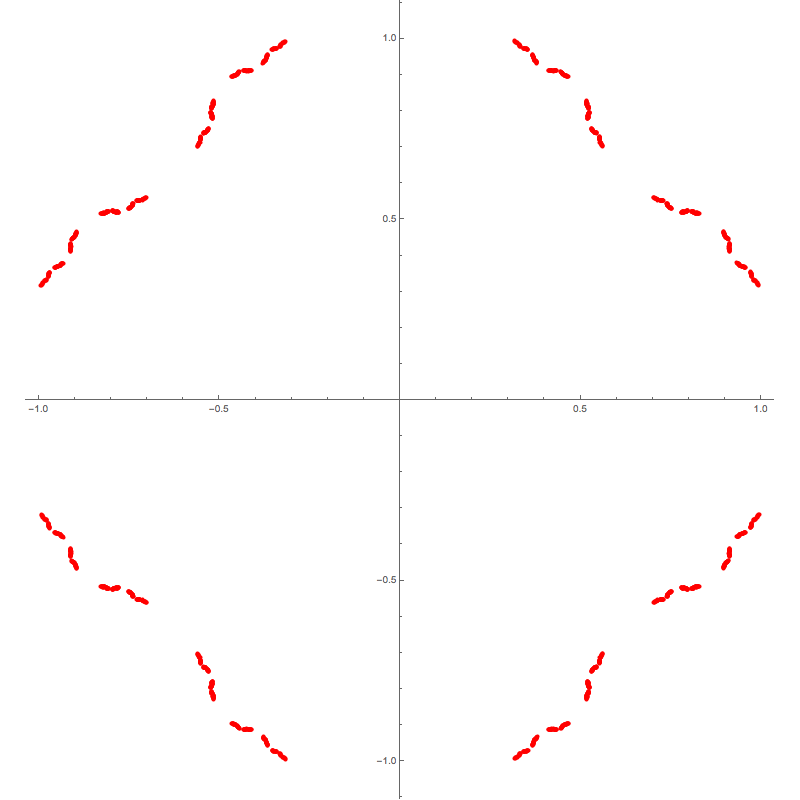
Fitting those points into the escape time image
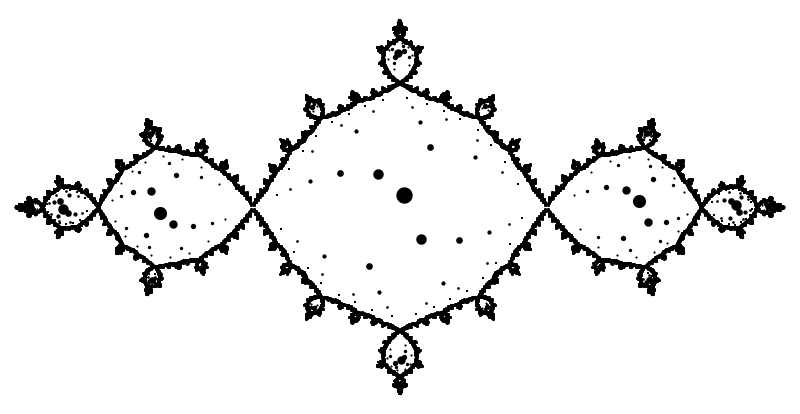
Improving inverse iteration by accounting for more inverses
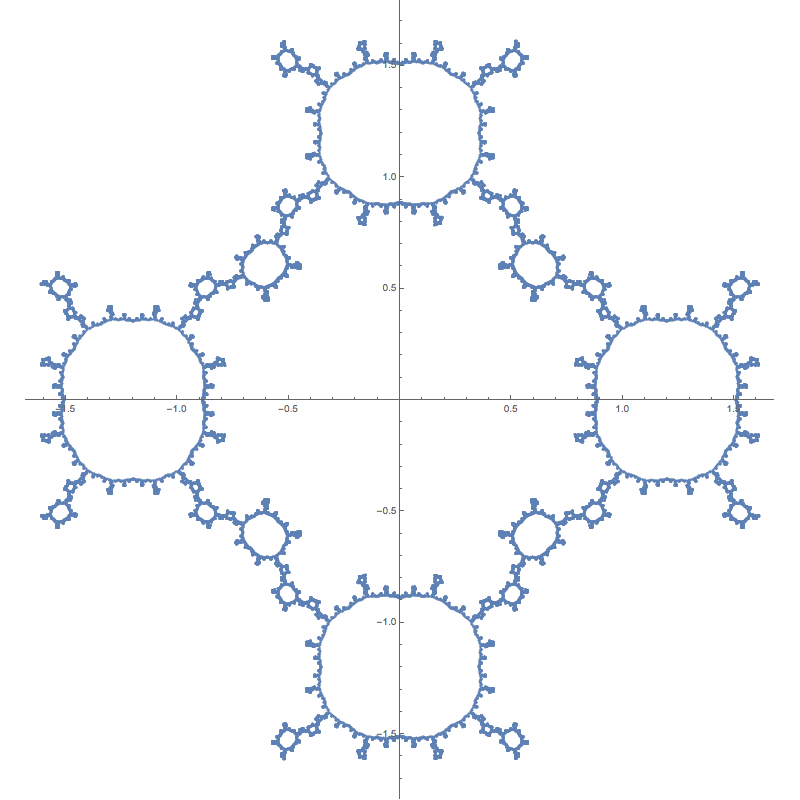
Attempting to get near the pole and highlihting the pre-images
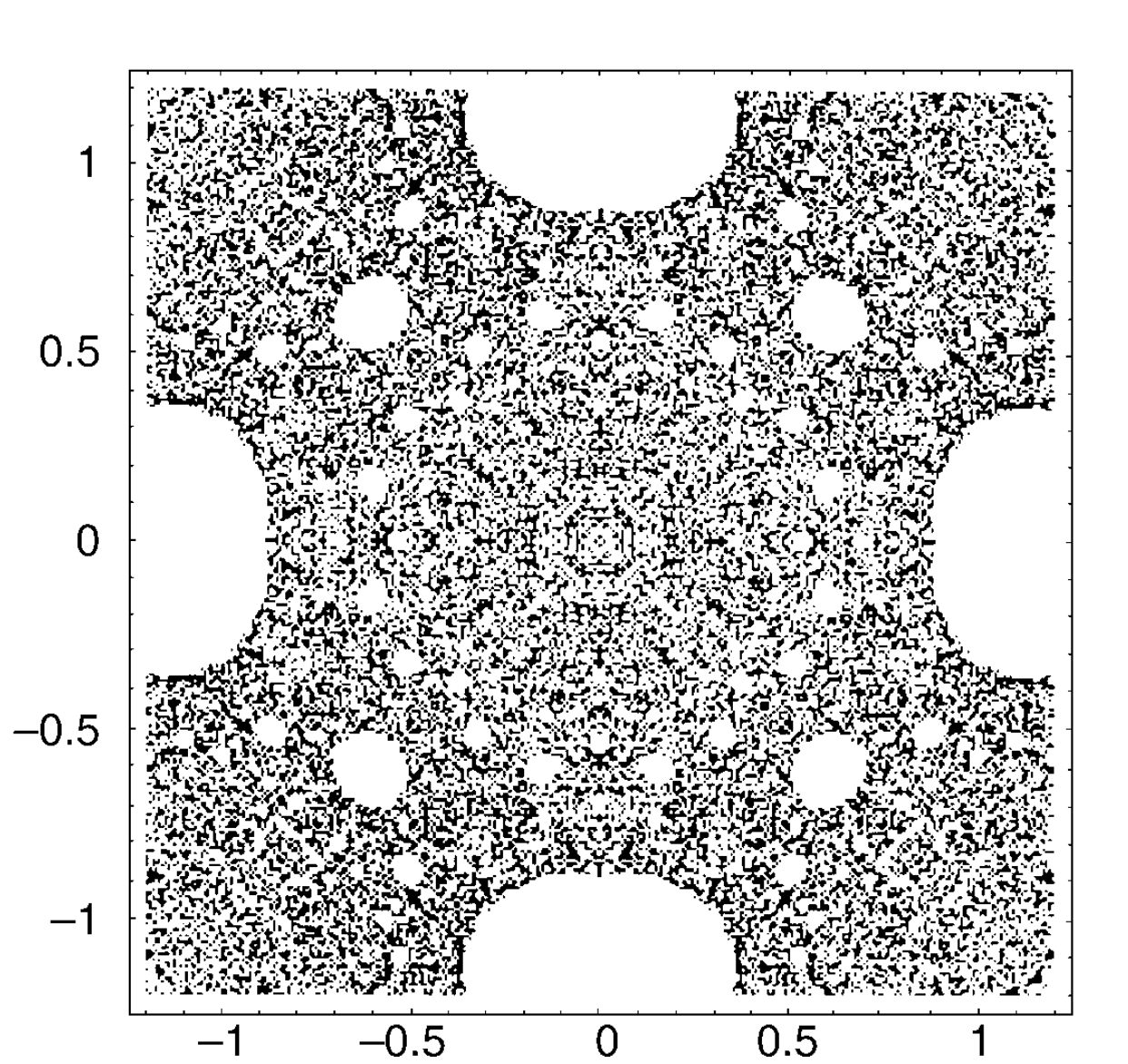
$g_2$-space
An escape time image for $g_2\approx3.18$ yielding a super attrative orbit of period 2.
An inverse iteration image for $g_2\approx3.18$
Parabolic dynamics
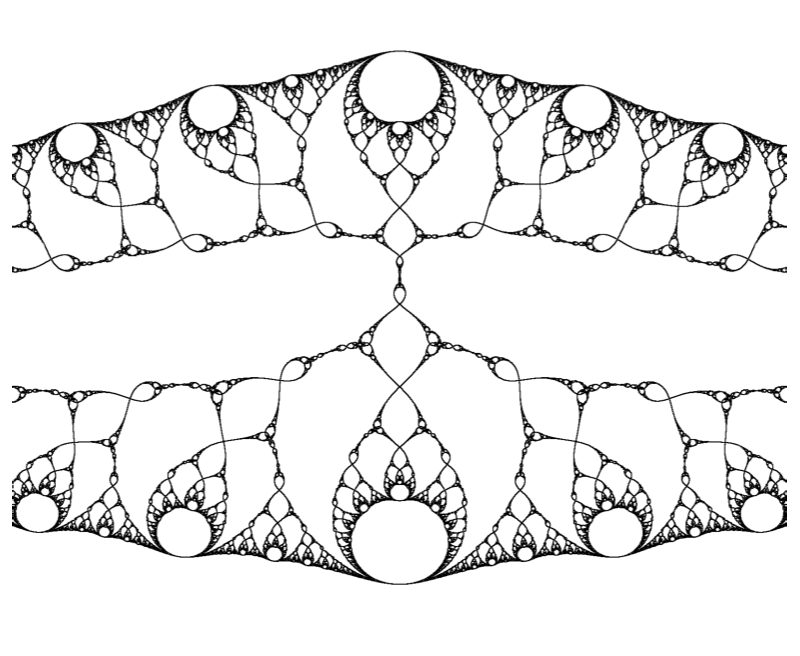$$R(z) = \frac{z^3-z}{1+4z-z^2}$$
A fixed point $z_0$ of the map $f$ is called parabolic if $f'(z_0)$ is a root of unity. We can extend this to a point with period $n$ by considering the map $f^n$.
Images involving parabolic dynamics can be difficult to generate since things move very slowly near the parabolic point.
Example: $f(z)=z-32z^5$?
A different approach
Scanning the boundary
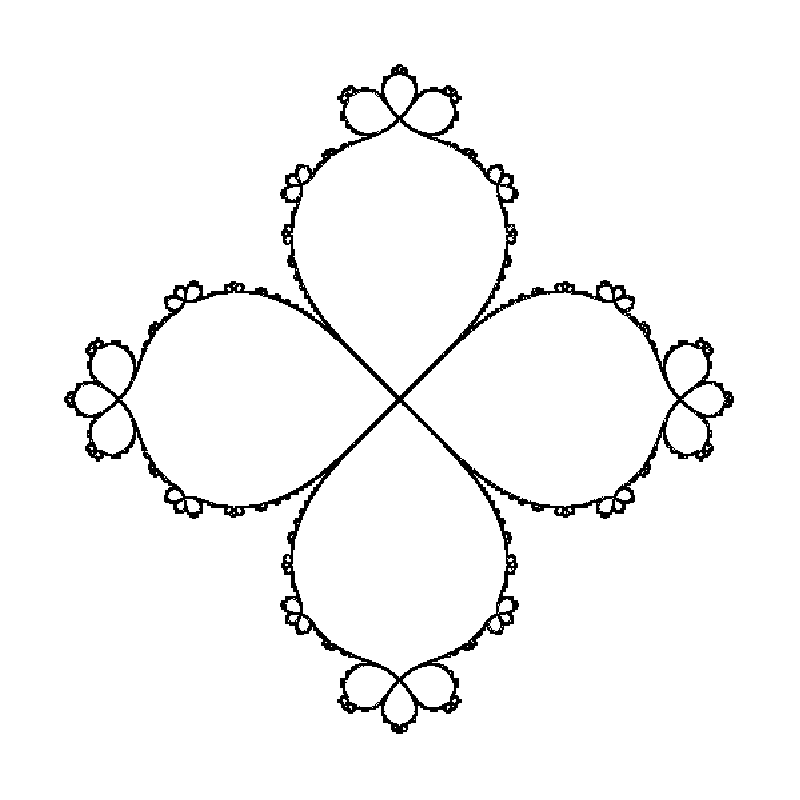
Now, for $$R(z) = \frac{z-z^3}{1+4z-z^2},$$ it turns out that $$R(R(z)) = z - 32 z^5 + O(z^6).$$ Thus, we might expect some similar behavior for $R$ near zero.
A closer look at the origin
